x2-11x+28=0: Unveiling the Mysteries of a Quadratic Equation
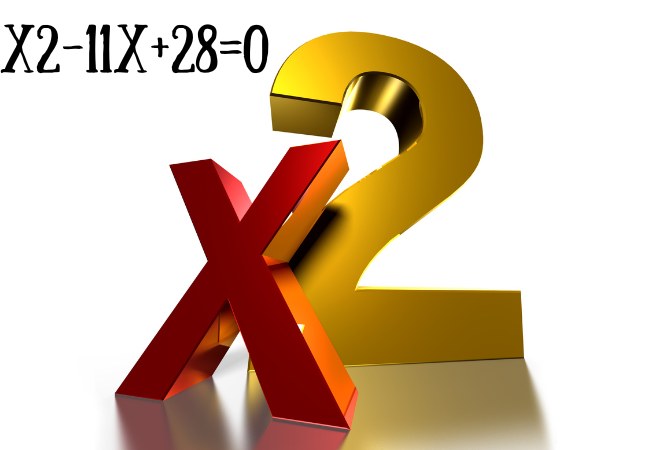
In the substantial expanse of mathematical equations, quadratic equations stand as poetic expressions of symmetry and elegance. Among them, x2-11x+28=0 emerges as a charming enigma, inviting us to unravel its secrets. Let us embark on a journey to decipher the mysteries hidden inside its coefficients and constants.
Understanding Quadratic Equations
Quadratic equations are problematic melodies composed of terms that resonate with profound mathematical importance. They take the form ax² + bx + c = zero, in which ‘a’, ‘b’, and ‘c’ are coefficients with particular roles to play. These equations often depict parabolic curves, shooting the essence of mathematical splendor.
Breaking Down x2-11x+28=0
Within the confines of x² – 11x + 28 = 0 lies a story ready to be instructed. The coefficient ‘1’ before x² indicates simplicity, while the coefficient ‘-eleven’ consists of the weight of complexity. The consistent ’28’ adds its very own flavor to the equation, finishing the narrative of mathematical poetry.
Finding Roots of the Quadratic Equation
Solving quadratic equations is comparable to unraveling a riddle, with a couple of methods at our disposal. Through meticulous calculations and algebraic manipulations, we will unearth the roots of x² – 11x + 28 = 0, revealing the answers hidden within its mathematical tapestry.
Graphical Representation
On the canvas of a graph, the equation x2-11x+28=0 paints a image of beauty and symmetry. Its curve gracefully dances throughout the axes, reflecting the intricate stability of its coefficients and constants. Through visualization, we benefit a deeper understanding of its essence.
Interpreting Solutions
As the solutions of x2-11x+28=0 emerge, they whisper stories of significance and relevance. Each root contains with it a message, illuminating the direction to comprehension in the realm of quadratic equations. Their interpretation transcends the boundaries of mathematics, resonating with real-life situations.
Comparing with Other Quadratic Equations
While x2-11x+28=0 stands specific in its own right, it is but one of a myriad of quadratic equations. Each equation tells its personal story, weaving a tapestry of mathematical diversity. By evaluating and contrasting, we gain a deeper appreciation for the nuances of quadratic expressions.
Applications
Quadratic equations find applications in diverse domain names, from physics to finance, from engineering to economics. Understanding x2-11x+28=0 unlocks doorways to a plethora of opportunities, empowering us to address real-world demanding situations with mathematical finesse.
Challenges and Pitfalls
Yet, the course to mastery isn’t always without its hurdles. Solving quadratic equations can be fraught with demanding situations, checking out the bounds of our mathematical prowess. However, with perseverance and resolution, we will triumph over those barriers and emerge positive in our quest for know-how.
Importance of Practice
Practice, they are saying, makes best. In the area of quadratic equations, this adage jewelry authentic. By immersing ourselves in the art of problem-solving, we hone our skills and sharpen our mind. Each equation turns into a canvas, inviting us to color the strokes of mathematical brilliance.
Exploring Further
As our adventure attracts to a close, allow us to not bid farewell, but as a substitute, embark on new adventures. Resources abound for the ones keen to delve deeper into the world of quadratic equations. Through exploration and inquiry, we hold to resolve the mysteries of mathematical splendor.
Conclusion
In the equation x2-11x+28=0, we discover not just numbers and logos, however a symphony of mathematical elegance. Its roots intertwine with the material of our know-how, guiding us on a adventure of discovery. Let us cherish the beauty of quadratic equations and embrace the information they communicate.
FAQs
What are the roots of the quadratic equation x2-11x+28=0?
The roots of this equation may be observed the use of various strategies together with factoring, finishing the rectangular, or the usage of the quadratic method.
How can I graphically represent the equation x2-11x+28=0?
Plotting the feature on a graph with x as the unbiased variable and y as the dependent variable will visually represent the parabolic curve corresponding to the equation.
What are a few actual-existence packages of quadratic equations?
Quadratic equations find packages in physics (e.G., projectile motion), engineering (e.G., structural design), economics (e.G., earnings optimization), and plenty of different fields.
How do I know if I’ve solved the quadratic equation effectively?
You can affirm your answers by means of substituting them again into the authentic equation and making sure that it satisfies the equation.
Are there any shortcuts for fixing quadratic equations faster?
While there aren’t any widely wide-spread shortcuts, familiarity with algebraic strategies and practice can considerably speed up the system of fixing quadratic equations.



